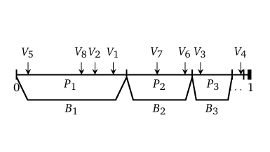
For the random interval partition of \([0,1]\) generated by the uniform stick-breaking scheme known as GEM\((1)\), let \(u_k\) be the probability that the first \(k\) intervals created by the stick-breaking scheme are also the first \(k\) intervals to be discovered in a process of uniform random sampling of points from \([0,1]\). Then \(u_k\) is a renewal sequence. We prove that \(u_k\) is a rational linear combination of the real numbers \(1, \zeta(2), \ldots, \zeta(k)\) where \(\zeta\) is the Riemann zeta function, and show that \(u_k\) has limit \(1/3\) as \(k \to \infty\). Related results provide probabilistic interpretations of some multiple zeta values in terms of a Markov chain derived from the interval partition. This Markov chain has the structure of a weak record chain. Similar results are given for the GEM\((\theta)\) model, with beta\((1,\theta)\) instead of uniform stick-breaking factors, and for another more algebraic derivation of renewal sequences from the Riemann zeta function.