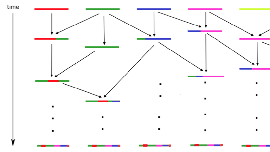
We consider a Moran model with recombination in a haploid population of size N. At each birth event, with probability 1−ρN the offspring copies one parent's chromosome, and with probability ρN she inherits a chromosome that is a mosaic of both parental chromosomes. We assume that at time 0 each individual has her chromosome painted in a different color and we study the color partition of the chromosome that is asymptotically fixed in a large population, when we look at a portion of the chromosome such that ρ:=limN→∞ρNN2→∞. To do so, we follow backwards in time the ancestry of the chromosome of a randomly sampled individual. This yields a Markov process valued in the color partitions of the half-line, that was introduced by \cite{esser}, in which blocks can merge and split, called the partitioning process. Its stationary distribution is closely related to the fixed chromosome in our Moran model with recombination. We are able to provide an approximation of this stationary distribution when ρ≫1 and an error bound. This allows us to show that the distribution of the (renormalised) length of the leftmost block of the partition (i.e. the region of the chromosome that carries the same color as 0) converges to an exponential distribution. In addition, the geometry of this block can be described in terms of a Poisson point process with an explicit intensity measure.